This is an old revision of the document!
PID Controller
PID - a proportional-integral-derivative or three-term controller is a mechanism to control process variable value, based on the feedback. Mainly used in systems and applications, which require to continuously control unstable value. As an example from everyday life, I can talk about cruise control systems in cars. The car brain, or main controller, compares the car's real speed with desired for hill ascending and descending. Then the PID algorithms are applied to control the engine power, i.e. increase or decrease it, to save vehicle resources. Also, we have applied PID algorithm in person detection experiment with drone. There we measured the difference between the detected person's bounding box center and image center and changed the yaw angle of the drone accordingly to minimize this error.
Main principles
The main definitions of the PID are the following. First, we have a desired setpoint (SP) - this is the value, that our process should maintain constantly. In drone experiment it was the difference between the centers, and it should be ideally be equal to 0. Second we have a real value of process variable (PV), that we get as an input to our PID algorithm. In drone experiment it was the real box centers' difference. So having two values we calculate the error, the difference we want to eliminate.
$$ SP= r(t) $$
$$ PV= y(t) $$
$$ e(t)= r(t) - y(t) $$
This is where PID algorithm start to work. the formula of it can be written as
PID = P + I + D
P Component
P is a proportional to the error value control. The larger the error, the larger the P, and vice versa. To adjust it koefficient Kp is used. But the main idea is that this control works only if there is an error.
P=Kp * e $$ P=K_{p} * e(t) $$
, where Kp is an adjustable coefficient.
I Component
I is an integral control. This component integrates or in other words, sums up all the past errors.
I=Ki*sum(e)
$$ I=K_{i}*\int_0^t \mathrm{e}(\tau)\,\mathrm{d}\tau $$
The main focus of I control is to eliminate residual error of system. When the error is close to 0, the integral component will stop growing.
D Component
D or derivative control is related to the speed of value change.
D = Kd*de/dt
$$ D=K_{d}*\frac{\mathrm{d}e(t)}{\mathrm{d}t} $$
here $$ \mathrm{d}e =e(t)-e(t-1) $$ dt is time since last change.
This value will be bigger with the lower time of change dt, meaning the faster value changes, the higher effect of D control would be felt. It is sometimes called “anticipatory control”, as it tries to estimate the future trend of value change based on current rate.
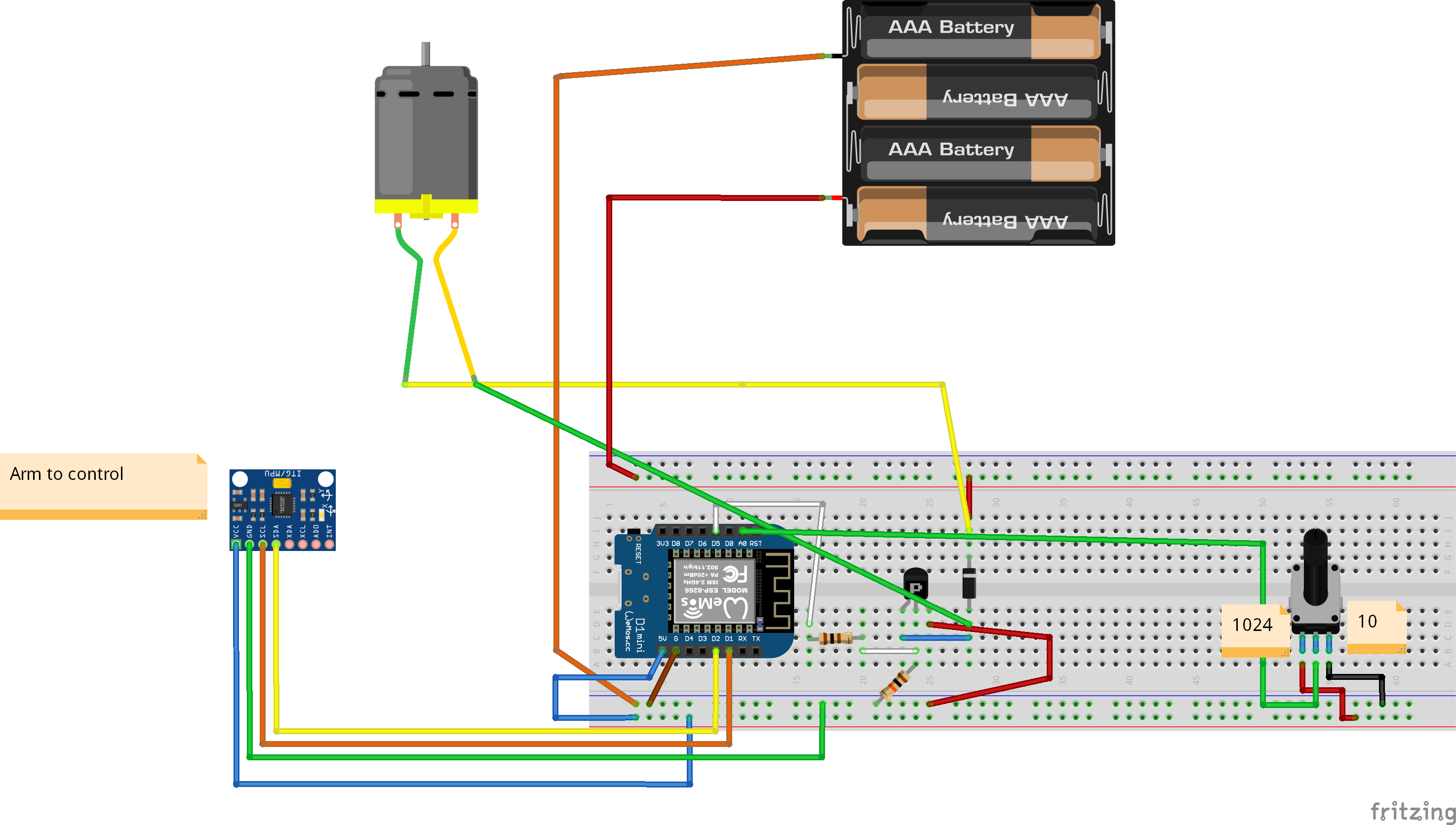
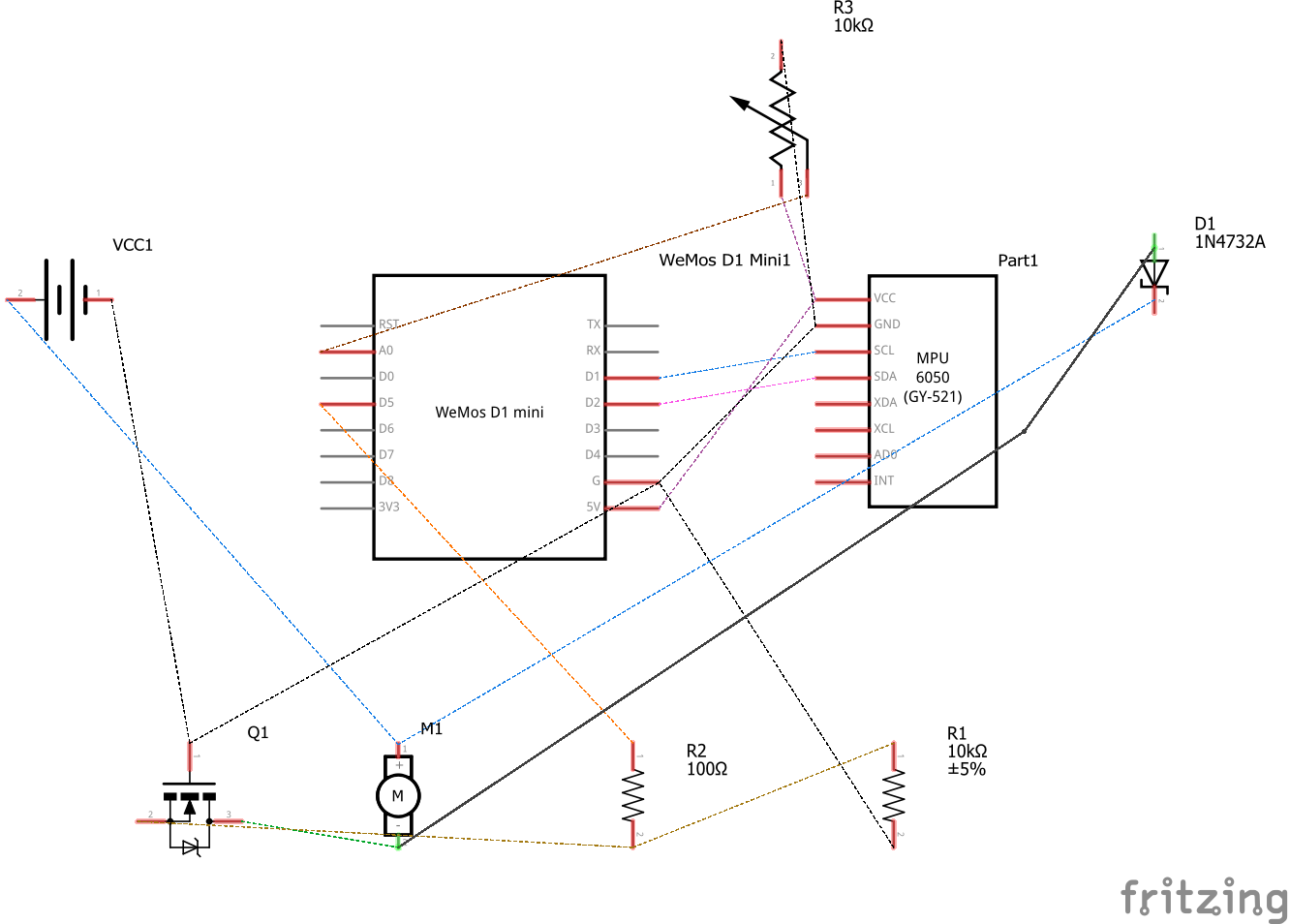
The Arm Schematic and components
Components:
- DC Motor
- ESP8266 controller
- MPU9250 sensor (placed on the arm)
- Potentiometer B10K, 10 kOm resistance
- Logic level mosfet
- 2 Resistors, 100 Om and 10 kOm
- Diod
- Power Station (settings: 3.8 Volts, Max Amper)
Arduino code
Built tool's limitations
Link to the code in GitHub repository https://github.com/eligosoftware/pid_arm_control/blob/main/sketch_apr29a_new_idea.ino
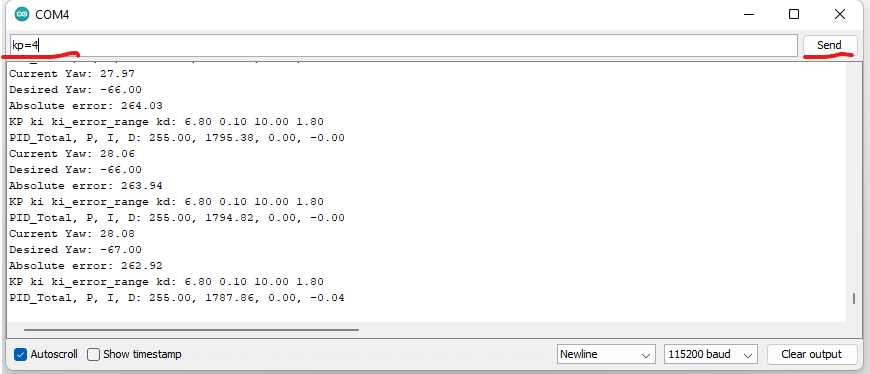
PID Tuning
Put together, the final formula of PID controller is:
PID = Kp * e + Ki*sum(e) + Kd*de/dt
$$ PID =K_{p} * e(t)+ K_{i}*\int_0^t \mathrm{e}(\tau)\,\mathrm{d}\tau + K_{d}*\frac{\mathrm{d}e(t)}{\mathrm{d}t} $$
From this formula you can see, that the only changable parts are K values. This tuning part is most important and most challenging, because generally PID doesn't guarantee optimal solution. There can always be lags in the response to the control, or the proportional relationship between SP and PV, for example, in drone example, between distance and yaw angle, can be incorrect. That is why the K coeffiecients should be manually tuned during experiments. One may find out, that some K values should be set to 0, this means this component is not applied at all. For example, if you set Ki value to 0, it means I
I=Ki*sum(e) will always be zero.
The commonly accepted way of tuning is following:
First you start changing Kp coefficient, and Ki Kd are set to 0. P value is proportional to error, and this leads to the oscilation of the system. To decrease the oscilations we can decrease Kp. If we want to react faster to changes, we need to take into account also the speed of changes, or Derivative controller D. Remember its formula